Robert Kordts-Freudinger

Sie haben mit Ihrem Fragebogen oder Beobachtungsbogen oder mit einer anderen Erhebungsmethode quantitative Daten gesammelt! Herzlichen Glückwunsch! Nun geht es darum, diese Daten sinnvoll auszuwerten.

Die deskriptive Auswertung der Daten geschieht in der Regel nicht auf der Ebene der einzelnen Fragen (Items), sondern auf der Ebene der Skalen (oder Subtests) Ihrer Erhebung. Die folgenden Kapitel beschreiben, wie Sie diese Skalen bilden können.

1. Warum Skalen bilden?

Ein Beispiel:

Sie haben 40 Schüler/innen zu ihrem Leseselbstkonzept und zu ihrer Lesemotivation mit einem Fragebogen befragt. Der Fragebogen hat 14 Items, von denen 8 das Leseselbstkonzept und 6 die Lesemotivation erfassen sollen. Die 5-stufige Antwortskala geht von ‚0‘ (trifft überhaupt nicht zu) bis ‚4‘ (trifft voll und ganz zu).

Wie im Beitrag zu Fragebögen kurz erklärt, bilden in der Regel mehrere Items eine Skala. Dies erhöht in der Regel die Reliabilität (Zuverlässigkeit) der Erfassung (siehe unten), die eine wichtige Voraussetzung für eine hohe Validität ist. Diese Skala und damit alle dazu gehörigen Items sollen ein Merkmal erfassen. In unserem Beispiel sollen also die 8 Items zusammen das Leseselbstkonzept erfassen.

Diese Skalen sollten die folgenden Eigenschaften aufweisen (Pospeschill, 2013, S. 114):

• verschiedene Schwierigkeiten der Items: Erfassung verschiedener Ausprägungsgrade des Merkmals
• hohe Reliabilität: verlässlich und genaue Messung
• hohe Trennschärfe der Items: Differenzierung von Personen mit hoher Merkmalsausprägung von Personen mit schwacher Merkmalsausprägung
• Homogenität (Dimensionalität): Die Items der Skala erfassen nur eine Dimension des theoretischen Konstrukts
• hohe Testobjektivität: eindeutig auswertbar
• hohe Testvalidität: gute Begründung dafür, dass auch wirklich das zu erfassende Konstrukt gemessen wird.

Die alles entscheidende Frage:

Treffen diese Eigenschaften auf Ihre Skala „Leseselbstkonzept“ wirklich zu?

Mithilfe einer Skalenanalyse können Sie Antworten zu den Aspekten der Item-Schwierigkeit, Reliabilität, Trennschärfe und Dimensionalität finden. Wie, wird im Folgenden dargestellt.

Achtung: In machen Fragebögen sind einige Items negativ gepolt. Im Beispiel ist Item Nr. 2 „Ich hasse das Lesen“ anders gepolt als die anderen Items dieser Skala. Wenn die generelle Richtung der Antwortskala eine positive ist, müssen Sie das negativ gepolte Item vor allen Berechnungen umpolen, d.h. niedrige Werte dieses Items durch gespiegelt hohe Werte ersetzen usw. (4 -> 0, 3 -> 1, 2 -> 2, 1 -> 3, 0 -> 4).

2. Item-Schwierigkeit

Zunächst empfehle ich Ihnen die Analyse der einzelnen Items. Hierfür bietet sich der Index der „Item-Schwierigkeit“ an. Dieser Index gibt an, von wie vielen Teilnehmenden das jeweilige Item mit hohen Werten beantwortet wird, also z.B. wie viele Teilnehmende mit „Ja“ oder „Stimme eher/voll zu“ geantwortet haben oder wie viele Teilnehmende die Multiple Choice-Aufgabe korrekt gelöst haben.

Berechnung:

Die Schwierigkeit wird bei Ratingskalen in der Regel wie der Mittelwert (s. Deskriptive Statistik) berechnet: Man summiert die Werte dieses einen Items über alle Teilnehmenden auf und teilt diese Summe durch die Anzahl der Teilnehmenden.

Voraussetzung für die Berechnung der Schwierigkeit als Mittelwert ist, dass die niedrigste Ausprägung des Items mit ‚0‘ kodiert ist und dass die höheren Werte aufsteigend mit ‚1‘, ‚2‘, ‚3‘ etc. kodiert sind. Wie oben gesagt, sollten die Schwierigkeiten der Items, die gemeinsam eine Skala bilden, einen möglichst breiten Bereich abdecken (möglichst unterschiedlich hoch sein). Dabei sollte es nicht zu viele Items mit extremen Schwierigkeiten geben.

Anmerkung:

Im Falle eines hohen Schwierigkeits-Werts (Mittelwerts) nennt man das Item „psychometrisch schwer“, bei niedrigen Werten „psychometrisch leicht“. Im Beispiel könnten also 2 der Items für die Skala Leseselbstkonzept eine niedrige Schwierigkeit (zwischen 0 und 1) aufweisen, z.B. das Item Nr. 3 „Das Lesen fällt mir immer extrem leicht.“

Daneben könnten 4 andere Items eine mittlere Schwierigkeit aufweisen (zwischen 1 und 3) und die restlichen 2 Items könnten eine hohe Schwierigkeit aufweisen (zwischen 3 und 4), z.B. das Item Nr. 5 „Lesefähigkeiten sind für mich später wichtig.“

3. Reliabilität

Da eine hohe Reliabilität wichtige Voraussetzung dafür ist, dass Sie Zusammenhänge und Unterschiede in Ihren Daten finden können, sollten Sie die Reliabilität Ihrer Skala bestimmen (s.a. Beitrag zur Planung).

Hierfür haben Sie verschiedene Rechen-Möglichkeiten. In diesem Kapitel konzentrieren wir uns auf die relativ leicht umsetzbaren Split-Half-Methode und die Methode der internen Konsistenz. Die auch möglichen Methoden Testwiederholung oder Paralleltest erklärt z.B. Bühner (2011, S. 235ff).

1. a) Split-half

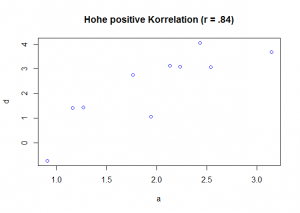
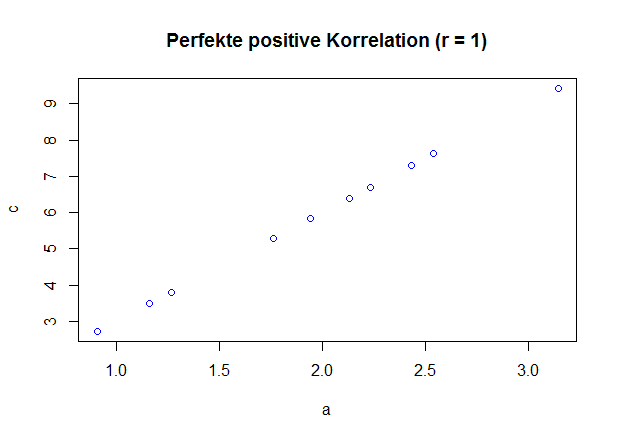
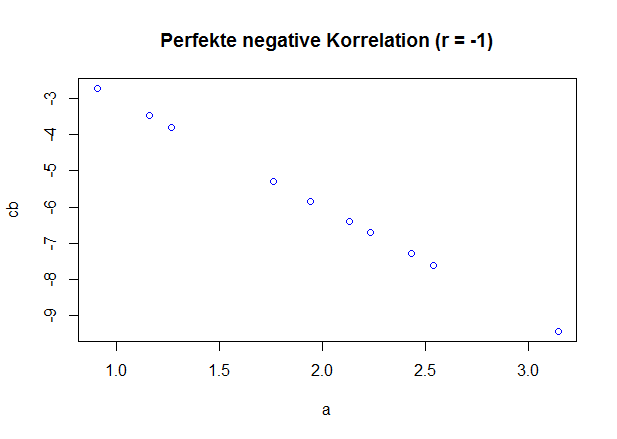
Bei dieser Rechnung wird die Skala, die Sie untersuchen, in zwei gleich große Hälften aufgeteilt und die Ergebnisse beider Hälften miteinander korreliert (in Zusammenhang gesetzt). Je höher die Korrelation zwischen beiden Hälften, desto zuverlässiger erfasst die Skala ein Konstrukt.

Achtung: WELCHES Konstrukt erfasst wird, ist hiermit noch nicht geklärt. Dies ist eine Frage der Validität.

Berechnung:

Sie können die Skala entweder nach 1. Hälfte und 2. Hälfte aufteilen oder (vor allem wenn die Skala aus sehr vielen Items besteht und die Antwortenden „ermüdet“ werden könnten) nach geraden und ungeraden Items aufteilen (sog. odd even-Methode).

Im Beispiel könnten Sie für die Skala Leseselbstkonzept eine Subskala mit allen Items mit einer ungeraden Nummer (Items Nummern 1, 3 und 5) und eine Subskala mit allen Items mit einer geraden Nummer (Items Nummern 2, 4 und 6) bilden. Die Skalenwerte dieser beiden Subskalen (z.B. Summen- oder Mittelwerte) korrelieren Sie dann miteinander. Weitere Details zum Vorgehen finden Sie z.B. bei Bühner (2011, S. 236).

1. b) Interne Konsistenz

Bei dieser – am häufigsten angewendeten – Berechnung der Reliabilität werden alle einzelnen Items miteinander korreliert und der Wert dieser Korrelation als Index für die Reliabilität interpretiert. Der am häufigsten genannte Index „Cronbachs Alpha“ gibt dabei den Wert der Reliabilität an: Je höher, desto besser.

Berechnung:

Der Kern der Formel für Cronbachs Alpha besteht aus den durchschnittlichen Korrelationen aller Items der Skala.

Generell gilt: Je mehr Items zu einer Skala gehören, desto höher Cronbachs Alpha.

Die Reliabilität sollte einen Wert von über .8 aufweisen. Ab einem Wert von .9 aufwärts spricht man von einer hohen Reliabilität (Bortz & Döring, 2006, S. 199). Alle Reliabilitäts-Werte unterhalb .7 benötigen daher einer Überarbeitung oder zumindest eines Überdenkens der Skala.

Im Beispiel könnte Cronbachs Alpha der Skala Leseselbstkonzept mit den Items in der Tabelle (siehe oben) eventuell nur einen Wert von .52 betragen. In so einem Fall können Sie versuchen, über das Weglassen einzelner Items, die wenig zum Wert beitragen, den Wert der Skala zu erhöhen (siehe Bühner, 2011).

4. Trennschärfe

Die Items einer Skala sollen – bei hoher Reliabilität – Personen mit niedriger Merkmalsausprägung (z.B. Schüler/innen mit einem schwach ausgeprägten Leseselbstkonzept) von solchen unterscheiden können, die eine hohe Merkmalsausprägung aufweisen (z.B. Schüler/innen mit einem stark ausgeprägten Leseselbstkonzept). Damit dieses Kriterium erfüllt ist, müssen die Items einer Skala trennscharf sein.

Berechnung:

Die Trennschärfe eines Items berechnet sich aus der Korrelation dieses Items mit dem Wert der Skala, zu der das Item gehören soll. Je höher der Wert, desto besser repräsentiert dieses Item die Gesamt-Skala, zu der es gehört.

Die Trennschärfe sollte einen Wert von über .5 aufweisen (Bortz & Döring, 2006, S. 220). Alle Items mit Trennschärfen-Werten unterhalb .3 benötigen daher einer Überarbeitung der Skala, z.B. durch Streichen der betroffenen Items.

Im Beispiel könnte die Trennschärfe des Items Nr. 4 „Lesen fällt mir sehr leicht“ der Skala Leseselbstkonzept einen Wert von .61 betragen. Dies würde inhaltlich bedeuten, dass Schüler/innen, denen (nach Selbstaussage) das Lesen leicht fällt, auch diejenigen sind, die generell ein positives Leseselbstkonzept aufweisen (zumindest mit der Skala „Leseselbstkonzept“). Ein niedriger (positiver) Wert von .13 oder sogar negative Werte wie -.23 würden bedeuten, dass Schüler/innen, denen das Lesen leicht fällt, wahrscheinlich kein positives Leseselbstkonzept haben, da die anderen Items in dieser Skala in eine andere Richtung deuten können.

5. Dimensionalität

Auch wenn die Items (z.B. Item Nr. 4 „Lesen fällt mir sehr leicht“) einer Skala (z.B. Leseselbstkonzept) mit genau dieser Skala hoch korrelieren (= eine hohe Trennschärfe aufweisen), kann es doch sein, dass sie auch mit den ANDEREN SKALEN ebenfalls hoch korrelieren (z.B. mit der Skala Lesemotivation). Alternativ könnte es auch sein, dass die Items Ihrer Skala (Leseselbstkonzept) gar nicht inhaltlich alle das Gleiche erfassen, sondern unterschiedliche Sachen. In der Regel sind diese beiden Fälle nicht erwünscht: Die Items eine Skala sollen „exklusiv“ zu dieser Skala gehören und nicht zu mehreren und pro Skala soll es nur eine inhaltliche Dimension geben. Vor allem dann, wenn eine dieser beiden Befürchtungen besteht und wenn Sie Items neu formuliert haben und bisher noch nicht empirisch getestet haben, sollten Sie deshalb eine Berechnung der Dimensionalität der Skalen vornehmen.

Hierfür wird in der Regel das statistische Verfahren der Faktorenanalyse (explorative oder konfirmatorische) durchgeführt.

Berechnung:

Die Faktorenanalyse bestimmt mittels verschiedener Verfahren die den Daten zugrundeliegenden Strukturen, die die Daten mit weniger als den ursprünglichen Items erklären können. Wenn mehrere Items das Gleiche erfassen, sollten sie auch hoch miteinander korrelieren. Die Faktorenanalyse bestimmt einen Faktor, der die gemeinsamen Anteile dieser miteinander korrelierenden Items repräsentiert (sozusagen den „Overlap“, das Gemeinsame dieser Items). Damit macht die Faktorenanalyse gleichzeitig die Struktur Ihrer Daten einfacher (weniger komplex). Ferner erhalten Sie im günstigen Fall dadurch die Bestätigung, dass den Items einer Skala (z.B. Leseselbstkonzept) wirklich nur ein gemeinsamer (in der Faktorenanalyse ermittelter) inhaltlicher Faktor zugrunde liegt. Das heißt, dass alle Items Ihrer Skala tatsächlich empirisch zusammenhängen und nicht zum Beispiel durch noch einen anderen Faktor erklärt werden können. Wenn es nur einen Faktor der Items einer Skala gibt, würden die Items Ihrer Skala „das Gleiche“ erfassen (WAS sie erfassen, das ist allerdings eine Frage der Validität!).

Details zur Faktorenanalyse inklusive aller Berechnungsschritte und Interpretationen finden Sie bei Bühner (2011, S. 295ff.).

Im Beispiel könnten Sie mittels der Faktorenanalyse aber auch herausfinden, dass – entgegen Ihrer Annahme – die ursprüngliche Skala Leseselbstkonzept tatsächlich aus zwei verschiedenen inhaltlichen Skalen besteht: der Skala „Leseselbstkonzept“ (z.B. mit dem Item Nr. 4 „Lesen fällt mir sehr leicht.“) und der Skala „Spaß am Lesen“ (z.B. mit dem Item Nr. 7 „Mir macht Lesen Freude.“). Diese beiden Dimensionen würden als „Faktoren“ oder „Komponenten“ vom Statistikprogramm ausgegeben werden. Sie würden daraufhin Ihre Skala „Leseselbstkonzept“ überarbeiten, hätten gleichzeitig aber auch eine neue Skala empirisch gefunden, mit der Sie weiterrechnen können. Mit Ihrer (neu gefundenen oder bestätigten) Skalenstruktur können Sie nun den Mittelwert (manchmal auch: die Summe) aller Items der Skala oder den Faktor aus der Faktorenanalyse als Skalenwert verwenden. Für diesen Skalenwert können Sie dann Mittelwerte und Standardabweichungen über die Antwortenden berechnen sowie andere deskriptive und inferenzstatistische Auswertungen vornehmen.

6. Ein Hinweis zum Schluss

Trotz aller mathematischen Berechnungen, die Sie mit Items und Skalen durchführen können und teilweise sollten, verlieren Sie nie die Semantik, den Inhalt der Items aus dem Blick. So kann man bei den oben aufgeführten Beispielen relativ schnell schon am Inhalt sehen, dass einige Items der Skala Leseselbstkonzept ganz andere Dimensionen erfassen als eben das Leseselbstkonzept und damit niedrige Trennschärfen, Reliabilitäten etc. berechnet werden (z.B. Items 1, 2, 7). Bei anderen Items sieht man schon an der Formulierung, dass sie sehr ähnliche Dinge erfassen (empirisch: hoch miteinander korrelieren werden und damit eins davon nicht nötig ist (z.B. Items 3 und 4). Diese inhaltlichen Erwägungen sind immer ein wichtiger Bestandteil der Item- und Skalenanalysen.

Software-Empfehlungen:

Für die Berechnung der in diesem Kapitel vorgestellten statistischen Verfahren empfehlen wir die Nutzung eines Statistik-Programms wie R oder SPSS.

https://www.youtube.com/watch?v=cX532N_XLIs&list=PLqzoL9-eJTNBDdKgJgJzaQcY6OXmsXAHU&index=1

Literatur

Bortz, J. & Döring, N. (2006). Forschungsmethoden und Evaluation für Human- und Sozialwissenschaftler (4. Aufl.). Berlin: Springer.

Bühner, M. (2011). Einführung in die Test- und Fragebogenkonstruktion (3. Aufl.). München: Pearson.

Pospeschill, M. (2013). Empirische Methoden in der Psychologie. München: UTB Reinhardt.

Carla Bohndick

Die deskriptive Statistik hilft Ihnen dabei, Ihre gesammelten Daten übersichtlich und anschaulich zusammenzufassen. Stellen Sie sich beispielsweise vor, Sie haben in Ihrer Befragung die demografischen Angaben Ihrer Versuchspersonen erhoben, vielleicht durch einen Fragebogen. Die deskriptive Statistik bietet Ihnen Kennwerte, die Ihnen dabei helfen, die Ergebnisse verdichtet darzustellen. Stellen wir uns also weiter vor, Sie haben das Alter Ihrer Versuchspersonen erhoben. Lagemaße (auch: Maße der zentralen Tendenz) geben nun an, welches Alter die Stichprobe am besten charakterisiert. Streuungsmaße (auch: Maße der Variabilität) zeigen die Unterschiedlichkeit der Stichprobe an.

Lagemaße

Die drei gebräuchlichsten Lagemaße sind das arithmetische Mittel, der Median und der Modus:

• Modus: definiert als derjenige Messwert, der am häufigsten in der Stichprobe vorkommt.
• Median: definiert als der Wert, der die Stichprobe in zwei Hälften teilt, wobei 50 % der Stichprobe größere (bzw. gleiche) Werte und 50% kleinere (bzw. gleiche)Werte aufweisen.
• Arithmetisches Mittel („Durchschnitt“): definiert als Summe der Werte in der Stichprobe, geteilt durch die Anzahl dieser Werte.

Streuungsmaße

• Range (Spannweite): Bereich vom kleinsten bis zum größten Wert, der in der Stichprobe auftritt
• Varianz: Mittelwert der quadrierten Abweichungen aller Einzelwerte vom Mittelwert der Verteilung (große Werte sprechen für eine hohe Unterschiedlichkeit der Messwerte in der Stichprobe, kleine für ähnliche Messwerte in der Stichprobe): 
• Standardabweichung: Wurzel der Varianz (die Interpretation der Standardabweichung ist einfacher als die der Varianz, da die Werte in der gleichen Einheit wie die der Messwerte verstanden werden können): 

Die Wahl des Lagemaßes und des Streuungsmaßes hängt vom Skalenniveau des gemessenen Merkmals, also der Variable ab:

Beispiel

Hier sehen Sie einen Ausschnitt aus einer Befragung zum Thema Motivation:

Zunächst müssen Sie die Skalenniveaus bestimmen:

• Nominal: Geschlecht
• Ordinal: Schulform
• Metrisch: Alter, Klasse, Mot1-Mot4

Anschließend können Sie die Lagemaße errechnen (hier der jeweils höchstwertigste):

• Geschlecht: W: 4 x vertreten; M: 3 x vorhanden; Modus: weiblich, d.h. die Mehrheit der befragten Personen ist weiblich. Weiblich ist also der Modalwert (= Modus).
• Alter:
   ;
  arithmetisches Mittel, d.h. im Schnitt sind die befragten Personen 9,86 Jahre alt
• Schulform: Zunächst wird jeder Schulform ein Wert zugeordnet, Hauptschule wird mit 1 und Gymnasium mit 3 belegt. Anschließend werden die Werte der Reihenfolge nach sortiert: 1,2,2,2,3,3,3. Der Wert in der Mitte ist der Median = 2, d.h. mindestens die Hälfte der Schüler/-innen ist mindestens auf der Realschule
• …

Schließlich berechnen Sie (wenn möglich) die Streuungsmaße:

• Geschlecht: –
• Alter:
  ,
  d.h. die durchschnittliche Abweichung des Alters vom Mittelwert 9.86 beträgt 0.69 Jahre.
  ,
  d.h. die jüngste Person ist 2 Jahre jünger als die älteste
• Schulform:
  ,
  d.h. die Person in der höchsten Schulform ist zwei Schulformen über der Person in der niedrigsten Schulform
• …

Software-Empfehlungen:

Sie können deskriptive Statistiken zwar per Hand berechnen, sobald Sie aber eine größere Stichprobe haben, wird dies relativ aufwendig. Daher empfiehlt es sich zumindest Tabellenkalkulationsprogramme wie bspw. Microsoft Excel oder Open-Office zu nutzen. Hier können Sie die Formeln „programmieren“, häufig stehen Ihnen aber auch bereits passende Funktionen zur Verfügung.

Sollten Sie besonderen Spaß an Statistik haben oder gerne weitere Berechnungen durchführen wollen, gibt es dafür spezielle Programme. Weit verbreitet sind dabei das kostenpflichtige Programm SPSS oder auch die kostenlose Open Source Statistik-Software R.

Literatur:

Beller, S. (2008). Empirisch forschen lernen. Konzepte, Methoden, Fallbeispiele, Tipps (2., überarb. Aufl). Bern: Huber.

Bortz, J. & Schuster, C. (2010). Statistik für Human- und Sozialwissenschaftler (7. Aufl.). Berlin: Springer.

Carla Bohndick

Wenn Sie untersuchen wollen, ob Zusammenhänge zwischen zwei Variablen bestehen, berechnen Sie die Korrelation. Zunächst ist dies eine deskriptive Fragestellung. Sie können die verschiedenen Zusammenhangsmaße aber auch inferenzstatistisch absichern. In diesem Kapitel wird verdeutlicht, was unter einer Korrelation verstanden wird. Außerdem werden Interpretationsprobleme dargestellt.

Die am häufigsten verwendete Möglichkeit, Zusammenhänge zwischen zwei Variablen zu berechnen, ist die Produkt-Moment-Korrelation. Um diese zu berechnen, müssen beide Variablen mindestens intervallskaliert sein. Im Folgenden berechnen wir die Korrelation zwischen dem Alter und der Motivation, genauer der Variable Mot 1 aus diesem Beitrag.

Zunächst müssen Sie die Kovarianz berechnen, die Formel dafür lautet:

Wenn Sie diese Formel genauer betrachten, fällt Ihnen sicherlich die Ähnlichkeit zu der in diesem Beitrag vorgestellten Varianz auf. Die Varianz ist nämlich lediglich die Kovarianz einer Variablen mit sich selber, also statt y würden Sie hier x einsetzen und so käme das Quadrat ins Spiel. Für unser Beispiel lässt sich also folgende Kovarianz berechnen:

Sei x = Alter und somit y= Mot1. Zuerst berechnen wir die Mittelwerte der Variablen x und y:

Nun können wir die Kovarianz berechnen:

Wir erhalten für unser Beispiel also eine Kovarianz von ca. 0,1776. Grundsätzlich kann die Kovarianz beliebig große Werte annehmen. Positive Werte sprechen dabei für einen positiven Zusammenhang zwischen den beiden Variablen und negative Werte für einen negativen Zusammenhang. Für unser Beispiel heißt das also, dass ein positiver Zusammenhang besteht.

Besser als die Kovarianz lässt sich die Korrelation (r) interpretieren. Für die Korrelation wird die Kovarianz anhand der Standardabweichungen (vgl. hier) der beiden Variablen standardisiert:

Zur Erinnerung: Die Standardabweichung ist gleich der Wurzel der Varianz.

Die Berechnung für unser Beispiel sieht also wie folgt aus:

Somit können wir r wie folgt berechnen:

Der Korrelationskoeffizient r kann Werte von -1 bis 1 annehmen. Bei -1 liegt ein perfekt negativer Zusammenhang vor, bei 0 liegt kein (linearer) Zusammenhang vor und bei 1 liegt ein perfekt positiver Zusammenhang vor. Welche Korrelationen als groß und welche Korrelationen als klein bezeichnet werden, lässt sich nicht abschließend bestimmen. Einige Autoren sehen Korrelationen ab 0.5 als groß, Korrelationen um 0.3 als moderat und Korrelationen um 0.1 als klein (Cohen, 1988), andere hingegen sehen Korrelationen bis 0.5 als gering, 0.7 als moderat und 0.9 als hoch an (Nachtigall & Wirtz, 2004). Letztlich kommt es auf den publizierten Forschungsstand zu einer konkreten Fragestellung an, welche Werte als bedeutsam betrachtet werden. Im sozialwissenschaftlichen Bereich ist es für neue Forschungsfragen üblich, von der genannten Konvention nach Cohen auszugehen. Für unser Beispiel gehen Sie bitte davon aus, dass Werte ab 0.3 als bedeutsam angesehen werden können. Das heißt also, dass zwischen dem Alter und der Variable Mot1 ein geringer positiver Zusammenhang besteht.

Um die verschieden starken Korrelationen besser zu illustrieren, finden Sie in den Abbildungen unten Beispiele für mögliche Korrelationen. Jeder Datenpunkt kann dabei einer Versuchsperson zugeordnet werden und zeigt damit das Ergebnis für zwei verschiedene Variablen an. Dabei ist die eine Variable auf der x-Achse und die andere Variable auf der y-Achse abgetragen.

Abb. 1 Verschiedene Korrelationen, Bewertung nach Cohen (1988)

Interpretationsprobleme: Korrelation und Kausalität

Stellen Sie sich vor, Sie hätten nun die Korrelation zwischen Leseleistung und Lesemotivation errechnet. Herausgekommen wäre r = 0.5, also ein moderater Zusammenhang zwischen den beiden Variablen. Sie können nun allerdings keine Aussagen über die Richtung des Zusammenhangs treffen. Das heißt, Aussagen wie „eine höhere Leseleistung führt zu einer höheren Lesemotivation“ oder andersherum „eine höhere Lesemotivation führt zu einer höheren Leseleistung“ sind nicht zulässig. Um Wirkrichtungen festzustellen, bedarf es spezieller Designs (vgl. Kapitel zur Planung). Manchmal ist auch eine dritte Variable z Auslöser für den Zusammenhang. Hier könnte z.B. die Begeisterung der Eltern für das Lesen (z) sowohl einen Einfluss auf die Lesemotivation (x) und auf die Leseleistung (y) haben, wie auch die folgende Abbildung veranschaulicht.

Um die Problematik zu verdeutlichen, sehen Sie im Folgenden weitere Beispiele, in denen fälschlicherweise eine bestimmte Richtung des Zusammenhangs angenommen wurde. Versuchen Sie doch einmal, die Gründe zu finden, die zu dem jeweiligen Zusammenhang geführt haben.

• Je mehr Leute der Feuerwehr eingesetzt werden, desto höher ist später der Brandschaden.
• Je größer die Füße, desto größer das Gehalt.
• Gute Luft (z.B. in Kurorten) führt zu einer erhöhten Sterblichkeitsrate.

Software-Empfehlungen:

Sie können Korrelationen per Hand berechnen, aber es gibt auch Computerprogramme, die Sie bei der Berechnung unterstützen können. Dies sind beispielsweise einfache Tabellenkalkulationsprogramme wie z.B. Excel, Sie können aber auch spezielle Software wie SPSS (kostenpflichtig) oder R (Open Source und kostenfrei) nutzen.

Literatur:

Beller, S. (2008). Empirisch forschen lernen. Konzepte, Methoden, Fallbeispiele, Tipps (2., überarb. Aufl). Bern: Huber.

Cohen, J. (1988). Statistical power analysis for the behavioral sciences (2. Aufl.). Hillsdale: L. Erlbaum Associates.

Krämer, W. (2009). So lügt man mit Statistik (12. Aufl.). München: Piper.

Nachtigall, C. & Wirtz, M. A. (2004). Wahrscheinlichkeitsrechnung und Inferenzstatistik (3. Aufl.). Weinheim: Juventa Verlag.

Carla Bohndick

Im Beitrag zur Deskriptiven Statistik haben Sie erfahren, wie Sie Ihre Daten beschreibend darstellen können. Häufig wollen Sie aber herausfinden, ob Ihre Daten Ihre postulierte Hypothese bestätigen (vgl. Kapitel zur Planung) Wenn Sie also beispielsweise die Hypothese aufgestellt haben, dass sich die Lesemotivation von Jungen und Mädchen unterscheidet, müssen Sie diese Hypothese prüfen.

Prüfung von Hypothesen

Das Grundprinzip zur Überprüfung ist immer ähnlich: Sie vergleichen, wie wahrscheinlich die von Ihnen gefundenen Kennwerte (z.B. Lagemaß, Streuungsmaß, Zusammenhangsmaß) sind, wenn man eine theoretisch angenommene Verteilung der Kennwerte zugrunde legt, mit einem per Konvention festgelegten Wahrscheinlichkeitswert (siehe unten „Signifikanz“). Diese zugrunde gelegte theoretische Verteilung wird als H0 (sprich: H-null) oder Nullhypothese bezeichnet, weil die Wahrscheinlichkeit für die gefundenen Kennwerte unter der Annahme berechnet wird, dass es null Unterschied zwischen den verglichenen Gruppen bzw. null Zusammenhang zwischen den untersuchten Variablen gibt. Die Annahmen, dass es dementgegen doch Unterschiede bzw. Zusammenhänge gibt, werden zusammenfassend als Alternativhypothese bzw. H1 bezeichnet.

Neben der Unterscheidung zwischen H0 bzw. H1 und Unterschieds- bzw. Zusammenhangshypothese wird auch noch nach ungerichteten bzw. gerichteten Hypothesen differenziert. Eine Hypothese ist ungerichtet, wenn die Alternativhypothesen sowohl positive als auch negative Abweichungen von der Nullannahme umfassen. Bei gerichteten Hypothesen ist festgelegt, dass nur Abweichungen in eine Richtung gegen die Nullhypothese sprechen, Abweichungen in die andere Richtung aber als für die Nullhypothese sprechend interpretiert werden (beispielsweise, weil sowohl Nullunterschiede als auch Abweichungen in die unerwartete Richtung gegen die inhaltlichen Forschungsannahmen sprechen).

Beispiele:

	H1	H0
Unterschiedshypothese ungerichtet	Es gibt einen Unterschied in der Lesemotivation von Jungen und Mädchen.	Es gibt keinen Unterschied in der Lesemotivation von Jungen und Mädchen.
Unterschiedshypothese gerichtet	Die Lesemotivation von Jungen ist höher als die von Mädchen.	Die Lesemotivation von Jungen ist kleiner oder gleich der Lesemotivation von Mädchen.
Zusammenhangshypothese ungerichtet	Die Lesemotivation hängt mit dem Alter der Schülerinnen und Schüler zusammen.	Die Lesemotivation hängt nicht mit dem Alter der Schülerinnen und Schüler zusammen.
Zusammenhangshypothese gerichtet	Die Lesemotivation steigt mit höherem Alter der Schülerinnen und Schüler.	Die Lesemotivation sinkt mit höherem Alter der Schülerinnen und Schüler oder bleibt gleich.

 Signifikanz

Im nächsten Schritt testen Sie, ob es Evidenz gegen – also Zweifel an der – Nullhypothese gibt. Die Logik dahinter ist, dass Sie es sich besonders schwer machen und die H0 so lange beibehalten, bis Sie sehr viel Evidenz gegen die H0 haben. Dies nennt sich Signifikanzprüfung. Dafür legen Sie ein Signifikanzniveau α fest (nach Konvention meist 5% oder 1%). Dies ist die Wahrscheinlichkeit, mit der die Nullhypothese abgelehnt wird, obwohl sie richtig ist. Wenn die errechnete Wahrscheinlichkeit kleiner ist als das vorher festgelegte Signifikanzniveau, heißt dies, dass Ihre Nullhypothese mit den Werten, die Sie erhoben haben, praktisch nicht vereinbar ist. Sie können H0 also verwerfen und die H1 akzeptieren.

Beispiel:

• Sie wollen die Hypothese überprüfen, dass es einen Unterschied in der Lesemotivation von Jungen und Mädchen gibt.
• Dafür stellen Sie die Nullhypothese „Es gibt keinen Unterschied zwischen Mädchen und Jungen“ auf.
• Das Signifikanzniveau legen Sie mit 5% (α = 0,05) fest.
• Durch einen passenden Signifikanztest (z.B. den unten vorgestellten t-Test) erhalten Sie eine Aussage über die Wahrscheinlichkeit, mit der Ihre Daten auftreten würden, wenn man die Nullhypothese annimmt, wenn es also keinen Unterschied zwischen Jungen und Mädchen gäbe.
• Ein Wert von 5,1% (p = 0,051) würde also dafür sprechen, die Nullhypothese beizubehalten, da diese nicht abgelehnt werden kann bzw. es nicht genug Evidenz gegen diese gibt.
• Demgegenüber würde ein Wert von 4,9% (p = 0,049) dafür sprechen, die Nullhypothese zu verwerfen. Sie könnten also feststellen, dass der Unterschied zwischen Mädchen und Jungen auf dem 5%-Niveau signifikant ist.

Verfahren zur Prüfung der Signifikanz bei Unterschiedshypothesen: Beispiel t-Test

Ein häufig angewandtes Verfahren, um Unterschiedshypothesen zu überprüfen, ist der t-Test. Dieser kann (leicht abgewandelt) für verschiedene Fragen verwendet werden:

• Unterscheidet sich der Mittelwert der Stichprobe zu einem Messzeitpunkt von dem Mittelwert derselben Stichprobe zu einem anderen Messzeitpunkt (Messwiederholung)? Sie könnte beispielsweise interessieren, ob sich die Leistung der Schülerinnen und Schüler vom Anfang bis zum Ende des Schuljahres verbessert hat.
• Unterscheidet sich der Mittelwert einer Stichprobe von dem Mittelwert einer anderen Stichprobe? Diese Frage ist beispielsweise dann interessant, wenn wie oben zwei Gruppen wie Mädchen oder Jungen oder Kinder der vierten Klasse und Kinder der fünften Klasse verglichen werden sollen.
• Unterscheidet sich der Mittelwert der Stichprobe von einem bestimmten gesetzten Wert? Diese Frage ist beispielsweise dann interessant, wenn Sie einen festgesetzten Wert haben und zum Beispiel untersuchen wollen, ob sich die maximale Konzentrationsfähigkeit von Schülerinnen und Schülern signifikant von einer Schulstunde von 45 Minuten unterscheidet.

Das Prinzip hinter dem t-Test ist wie folgt: Aus den Mittelwerten und der Standardabweichung (also statistischen Kennwerten) wird ein Wert (der Testwert) berechnet. Dieser Wert wird anschließend mit einer Verteilung verglichen.

Bei unserem Beispiel handelt es sich um zwei unabhängige Stichproben, also die Stichprobe der Jungen und die Stichprobe der Mädchen. Für den Fall, dass Sie gleich viele Mädchen wie Jungen befragt haben, die Stichproben also gleich groß sind, lautet die Formel wie folgt:

Im Zähler steht die Differenz der Mittelwerte. In unserem Beispiel wäre das also der Mittelwert der Lesemotivation der Jungen, der von dem Mittelwert der Lesemotivation der Mädchen abgezogen wird. Um den Nenner zu berechnen, brauchen Sie die Gesamtstichprobengröße n sowie die Varianz s² beider Gruppen. Wie Sie diese berechnen, können Sie hier nachlesen. Das Ergebnis ist Ihr Testwert t, den Sie nun mit dem kritischen t-Wert vergleichen. Dieser kritische t-Wert wird berechnet, indem die H0, dass es keine Unterschiede zwischen den Gruppen gibt, zugrunde gelegt wird. Wenn Sie einen empirischen t-Wert aus Ihren Daten berechnet haben, der extremer ist als der kritische t-Wert, dann bedeutet dies, dass Ihre gefundenen Daten sehr schlecht zu der Annahme passen, dass es keine Unterschiede gibt. Sie lehnen deswegen in diesem Fall die H0 ab. Um den kritischen t-Wert herauszufinden, können Sie Verteilungsfunktionen heranziehen, die in Statistiklehrbüchern in Tabellenform abgedruckt sind. Diese Aufgabe übernimmt Ihre Statistiksoftware (s. Softwareempfehlungen) aber auch für Sie. Wichtig ist in beiden Fällen, dass Sie beachten, ob Ihre Forschungshypothese gerichtet oder ungerichtet ist. Zu gerichteten Hypothesen gehören einseitige Testungen bzw. die unmittelbar ablesbaren Signifikanz-Grenzen und zu ungerichteten Hypothesen zweiseitige Testungen bzw. die halbierten tabellierten Signifikanz-Grenzen (sofern die Tabellen für einseitige Testungen ausgelegt sind).

Voraussetzung für den t-Test ist, dass das Merkmal normalverteilt oder Ihre Stichprobe groß genug ist. Falls dies bei Ihnen nicht der Fall ist, stehen Ihnen nonparametrische Verfahren zur Verfügung, die nach ähnlichen Prinzipien funktionieren. Auch für weitere Fragestellungen, wie klassische Evaluationsdesigns (vgl. Planung von Studien), existieren passende Methoden, wie z.B. die Varianzanalyse mit Messwiederholung. Auch Zusammenhangshypothesen werden nach demselben Verfahren (statistischen Kennwerte – Testwerte – Vergleich mit Verteilung) geprüft.

Effektstärke

Die Signifikanz ist u.a. von der Stichprobengröße abhängig, bei sehr großen Stichproben werden auch kleinste Effekte signifikant, bei sehr kleinen Stichproben auch große nicht. Deshalb ist es sinnvoll, wenn Sie zusätzlich zur Signifikanz auch Effektstärken berichten. Darunter können standardisierte Kennwerte verstanden werden, die beispielsweise Aussagen über die Relevanz von Mittelwertunterschieden machen.  Durch die Standardisierung ist es möglich, Ergebnisse verschiedener Studien zu vergleichen und zusammen zu fassen.

Ein Beispiel dafür ist Cohens d, eine Effektgröße für Mittelwertunterschiede. Wenn die beiden Gruppen, die Sie vergleichen, dieselbe Gruppengröße n haben, wird der Wert mit folgender Rechnung geschätzt:

Ähnlich wie bei der Formel zur Berechnung des t-Wertes steht dabei im Zähler wieder die Differenz der Mittelwerte, im Nenner stehen die Varianzen. Der Unterschied ist, dass hier nicht durch die Stichprobe geteilt wird (s.o.). Ihr Ergebnis können Sie folgendermaßen interpretieren: kleiner Effekt: d = 0,2; mittlerer Effekt: d = 0,5; großer Effekt: d = 0,8 (Cohen, 1988).

Eine Effektstärke für Zusammenhangshypothesen ist r und wird im Kapitel Zusammenhangsmaße eingeführt.

Softwareempfehlungen:

Zur Prüfung von Hypothesen bietet sich die Nutzung spezieller Statistiksoftware wie SPSS (kostenpflichtig) oder R (kostenfrei) an. Effektstärken werden häufig nicht angegeben. Diese können Sie sich aber einfach mit Tabellenkalkulationsprogrammen programmieren oder mit dem Taschenrechner per Hand ausrechnen.

Literaturempfehlungen:

Beller, S. (2008). Empirisch forschen lernen. Konzepte, Methoden, Fallbeispiele, Tipps (2., überarb. Aufl). Bern: Huber.

Bortz, J. & Döring, N. (2006). Forschungsmethoden und Evaluation. Für Human- und Sozialwissenschaftler (4. Aufl.). Heidelberg: Springer.

Bortz, J. & Schuster, C. (2010). Statistik für Human- und Sozialwissenschaftler (7. Aufl.). Berlin: Springer.

Cohen, J. (1988). Statistical power analysis for the behavioral sciences (2. Aufl.). Hillsdale: L. Erlbaum Associates.