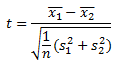Carla Bohndick

Im Beitrag zur Deskriptiven Statistik haben Sie erfahren, wie Sie Ihre Daten beschreibend darstellen können. Häufig wollen Sie aber herausfinden, ob Ihre Daten Ihre postulierte Hypothese bestätigen (vgl. Kapitel zur Planung) Wenn Sie also beispielsweise die Hypothese aufgestellt haben, dass sich die Lesemotivation von Jungen und Mädchen unterscheidet, müssen Sie diese Hypothese prüfen.

Prüfung von Hypothesen

Das Grundprinzip zur Überprüfung ist immer ähnlich: Sie vergleichen, wie wahrscheinlich die von Ihnen gefundenen Kennwerte (z.B. Lagemaß, Streuungsmaß, Zusammenhangsmaß) sind, wenn man eine theoretisch angenommene Verteilung der Kennwerte zugrunde legt, mit einem per Konvention festgelegten Wahrscheinlichkeitswert (siehe unten „Signifikanz“). Diese zugrunde gelegte theoretische Verteilung wird als H0 (sprich: H-null) oder Nullhypothese bezeichnet, weil die Wahrscheinlichkeit für die gefundenen Kennwerte unter der Annahme berechnet wird, dass es null Unterschied zwischen den verglichenen Gruppen bzw. null Zusammenhang zwischen den untersuchten Variablen gibt. Die Annahmen, dass es dementgegen doch Unterschiede bzw. Zusammenhänge gibt, werden zusammenfassend als Alternativhypothese bzw. H1 bezeichnet.

Neben der Unterscheidung zwischen H0 bzw. H1 und Unterschieds- bzw. Zusammenhangshypothese wird auch noch nach ungerichteten bzw. gerichteten Hypothesen differenziert. Eine Hypothese ist ungerichtet, wenn die Alternativhypothesen sowohl positive als auch negative Abweichungen von der Nullannahme umfassen. Bei gerichteten Hypothesen ist festgelegt, dass nur Abweichungen in eine Richtung gegen die Nullhypothese sprechen, Abweichungen in die andere Richtung aber als für die Nullhypothese sprechend interpretiert werden (beispielsweise, weil sowohl Nullunterschiede als auch Abweichungen in die unerwartete Richtung gegen die inhaltlichen Forschungsannahmen sprechen).

Beispiele:

	H1	H0
Unterschiedshypothese ungerichtet	Es gibt einen Unterschied in der Lesemotivation von Jungen und Mädchen.	Es gibt keinen Unterschied in der Lesemotivation von Jungen und Mädchen.
Unterschiedshypothese gerichtet	Die Lesemotivation von Jungen ist höher als die von Mädchen.	Die Lesemotivation von Jungen ist kleiner oder gleich der Lesemotivation von Mädchen.
Zusammenhangshypothese ungerichtet	Die Lesemotivation hängt mit dem Alter der Schülerinnen und Schüler zusammen.	Die Lesemotivation hängt nicht mit dem Alter der Schülerinnen und Schüler zusammen.
Zusammenhangshypothese gerichtet	Die Lesemotivation steigt mit höherem Alter der Schülerinnen und Schüler.	Die Lesemotivation sinkt mit höherem Alter der Schülerinnen und Schüler oder bleibt gleich.

 Signifikanz

Im nächsten Schritt testen Sie, ob es Evidenz gegen – also Zweifel an der – Nullhypothese gibt. Die Logik dahinter ist, dass Sie es sich besonders schwer machen und die H0 so lange beibehalten, bis Sie sehr viel Evidenz gegen die H0 haben. Dies nennt sich Signifikanzprüfung. Dafür legen Sie ein Signifikanzniveau α fest (nach Konvention meist 5% oder 1%). Dies ist die Wahrscheinlichkeit, mit der die Nullhypothese abgelehnt wird, obwohl sie richtig ist. Wenn die errechnete Wahrscheinlichkeit kleiner ist als das vorher festgelegte Signifikanzniveau, heißt dies, dass Ihre Nullhypothese mit den Werten, die Sie erhoben haben, praktisch nicht vereinbar ist. Sie können H0 also verwerfen und die H1 akzeptieren.

Beispiel:

• Sie wollen die Hypothese überprüfen, dass es einen Unterschied in der Lesemotivation von Jungen und Mädchen gibt.
• Dafür stellen Sie die Nullhypothese „Es gibt keinen Unterschied zwischen Mädchen und Jungen“ auf.
• Das Signifikanzniveau legen Sie mit 5% (α = 0,05) fest.
• Durch einen passenden Signifikanztest (z.B. den unten vorgestellten t-Test) erhalten Sie eine Aussage über die Wahrscheinlichkeit, mit der Ihre Daten auftreten würden, wenn man die Nullhypothese annimmt, wenn es also keinen Unterschied zwischen Jungen und Mädchen gäbe.
• Ein Wert von 5,1% (p = 0,051) würde also dafür sprechen, die Nullhypothese beizubehalten, da diese nicht abgelehnt werden kann bzw. es nicht genug Evidenz gegen diese gibt.
• Demgegenüber würde ein Wert von 4,9% (p = 0,049) dafür sprechen, die Nullhypothese zu verwerfen. Sie könnten also feststellen, dass der Unterschied zwischen Mädchen und Jungen auf dem 5%-Niveau signifikant ist.

Verfahren zur Prüfung der Signifikanz bei Unterschiedshypothesen: Beispiel t-Test

Ein häufig angewandtes Verfahren, um Unterschiedshypothesen zu überprüfen, ist der t-Test. Dieser kann (leicht abgewandelt) für verschiedene Fragen verwendet werden:

• Unterscheidet sich der Mittelwert der Stichprobe zu einem Messzeitpunkt von dem Mittelwert derselben Stichprobe zu einem anderen Messzeitpunkt (Messwiederholung)? Sie könnte beispielsweise interessieren, ob sich die Leistung der Schülerinnen und Schüler vom Anfang bis zum Ende des Schuljahres verbessert hat.
• Unterscheidet sich der Mittelwert einer Stichprobe von dem Mittelwert einer anderen Stichprobe? Diese Frage ist beispielsweise dann interessant, wenn wie oben zwei Gruppen wie Mädchen oder Jungen oder Kinder der vierten Klasse und Kinder der fünften Klasse verglichen werden sollen.
• Unterscheidet sich der Mittelwert der Stichprobe von einem bestimmten gesetzten Wert? Diese Frage ist beispielsweise dann interessant, wenn Sie einen festgesetzten Wert haben und zum Beispiel untersuchen wollen, ob sich die maximale Konzentrationsfähigkeit von Schülerinnen und Schülern signifikant von einer Schulstunde von 45 Minuten unterscheidet.

Das Prinzip hinter dem t-Test ist wie folgt: Aus den Mittelwerten und der Standardabweichung (also statistischen Kennwerten) wird ein Wert (der Testwert) berechnet. Dieser Wert wird anschließend mit einer Verteilung verglichen.

Bei unserem Beispiel handelt es sich um zwei unabhängige Stichproben, also die Stichprobe der Jungen und die Stichprobe der Mädchen. Für den Fall, dass Sie gleich viele Mädchen wie Jungen befragt haben, die Stichproben also gleich groß sind, lautet die Formel wie folgt:

Im Zähler steht die Differenz der Mittelwerte. In unserem Beispiel wäre das also der Mittelwert der Lesemotivation der Jungen, der von dem Mittelwert der Lesemotivation der Mädchen abgezogen wird. Um den Nenner zu berechnen, brauchen Sie die Gesamtstichprobengröße n sowie die Varianz s² beider Gruppen. Wie Sie diese berechnen, können Sie hier nachlesen. Das Ergebnis ist Ihr Testwert t, den Sie nun mit dem kritischen t-Wert vergleichen. Dieser kritische t-Wert wird berechnet, indem die H0, dass es keine Unterschiede zwischen den Gruppen gibt, zugrunde gelegt wird. Wenn Sie einen empirischen t-Wert aus Ihren Daten berechnet haben, der extremer ist als der kritische t-Wert, dann bedeutet dies, dass Ihre gefundenen Daten sehr schlecht zu der Annahme passen, dass es keine Unterschiede gibt. Sie lehnen deswegen in diesem Fall die H0 ab. Um den kritischen t-Wert herauszufinden, können Sie Verteilungsfunktionen heranziehen, die in Statistiklehrbüchern in Tabellenform abgedruckt sind. Diese Aufgabe übernimmt Ihre Statistiksoftware (s. Softwareempfehlungen) aber auch für Sie. Wichtig ist in beiden Fällen, dass Sie beachten, ob Ihre Forschungshypothese gerichtet oder ungerichtet ist. Zu gerichteten Hypothesen gehören einseitige Testungen bzw. die unmittelbar ablesbaren Signifikanz-Grenzen und zu ungerichteten Hypothesen zweiseitige Testungen bzw. die halbierten tabellierten Signifikanz-Grenzen (sofern die Tabellen für einseitige Testungen ausgelegt sind).

Voraussetzung für den t-Test ist, dass das Merkmal normalverteilt oder Ihre Stichprobe groß genug ist. Falls dies bei Ihnen nicht der Fall ist, stehen Ihnen nonparametrische Verfahren zur Verfügung, die nach ähnlichen Prinzipien funktionieren. Auch für weitere Fragestellungen, wie klassische Evaluationsdesigns (vgl. Planung von Studien), existieren passende Methoden, wie z.B. die Varianzanalyse mit Messwiederholung. Auch Zusammenhangshypothesen werden nach demselben Verfahren (statistischen Kennwerte – Testwerte – Vergleich mit Verteilung) geprüft.

Effektstärke

Die Signifikanz ist u.a. von der Stichprobengröße abhängig, bei sehr großen Stichproben werden auch kleinste Effekte signifikant, bei sehr kleinen Stichproben auch große nicht. Deshalb ist es sinnvoll, wenn Sie zusätzlich zur Signifikanz auch Effektstärken berichten. Darunter können standardisierte Kennwerte verstanden werden, die beispielsweise Aussagen über die Relevanz von Mittelwertunterschieden machen.  Durch die Standardisierung ist es möglich, Ergebnisse verschiedener Studien zu vergleichen und zusammen zu fassen.

Ein Beispiel dafür ist Cohens d, eine Effektgröße für Mittelwertunterschiede. Wenn die beiden Gruppen, die Sie vergleichen, dieselbe Gruppengröße n haben, wird der Wert mit folgender Rechnung geschätzt:

Ähnlich wie bei der Formel zur Berechnung des t-Wertes steht dabei im Zähler wieder die Differenz der Mittelwerte, im Nenner stehen die Varianzen. Der Unterschied ist, dass hier nicht durch die Stichprobe geteilt wird (s.o.). Ihr Ergebnis können Sie folgendermaßen interpretieren: kleiner Effekt: d = 0,2; mittlerer Effekt: d = 0,5; großer Effekt: d = 0,8 (Cohen, 1988).

Eine Effektstärke für Zusammenhangshypothesen ist r und wird im Kapitel Zusammenhangsmaße eingeführt.

 

Softwareempfehlungen:

Zur Prüfung von Hypothesen bietet sich die Nutzung spezieller Statistiksoftware wie SPSS (kostenpflichtig) oder R (kostenfrei) an. Effektstärken werden häufig nicht angegeben. Diese können Sie sich aber einfach mit Tabellenkalkulationsprogrammen programmieren oder mit dem Taschenrechner per Hand ausrechnen.

 

Literaturempfehlungen:

Beller, S. (2008). Empirisch forschen lernen. Konzepte, Methoden, Fallbeispiele, Tipps (2., überarb. Aufl). Bern: Huber.

Bortz, J. & Döring, N. (2006). Forschungsmethoden und Evaluation. Für Human- und Sozialwissenschaftler (4. Aufl.). Heidelberg: Springer.

Bortz, J. & Schuster, C. (2010). Statistik für Human- und Sozialwissenschaftler (7. Aufl.). Berlin: Springer.

Cohen, J. (1988). Statistical power analysis for the behavioral sciences (2. Aufl.). Hillsdale: L. Erlbaum Associates.