Carla Bohndick

Wenn Sie quantitative Daten erhoben und ausgewertet haben, ist es in vielen Fällen sinnvoll, diese auch mit Hilfe von Grafiken darzustellen, beispielsweise um Verteilungen oder Unterschiede zwischen Gruppen anschaulich zu machen. Im Folgenden werden Ihnen zwei Möglichkeiten dazu vorgestellt, wobei wir uns hier auf die Darstellung univariater Verteilungen (also der Verteilung eines einzelnen Merkmals) beschränken. Sie können natürlich auch bivariate Verteilungen (also die Verteilung zweier Merkmale) grafisch darstellen, beachten Sie dafür die folgenden Hinweise und die Literaturempfehlungen.

Histogramm:

Bei einem Histogramm wird die Verteilung einer Variablen mit direkt angrenzenden Säulen dargestellt. Dabei sind auf der x-Achse die Kategorien (z.B. Punktzahl oder Alter) abgetragen. Auf der y-Achse sind entweder absolute oder relative Häufigkeiten (z.B. in Prozent) abgetragen. Die Darstellung ist flächenproportional, d.h. die Fläche der Säulen entspricht der Häufigkeit der jeweiligen Kategorien. Histogramme können Sie zur Visualisierung von Häufigkeitsverteilungen nutzen.

Beispiel:

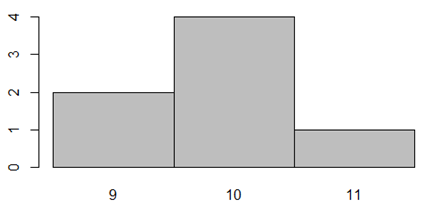
Unten sehen Sie ein Beispiel-Histogramm, das aus den Daten diesem Beitrag gebildet wurde. Auf der x-Achse sind die Altersangaben 9, 10 und 11 abgebildet, die y-Achse gibt die absolute Häufigkeit der Altersangaben an, d.h. wie viele Personen es in der entsprechenden Altersstufe in der betrachteten Gruppe gibt. Erkennbar ist, dass zwei Personen 9 Jahre alt waren, vier Personen 10 Jahre alt und eine Person 11 Jahre alt.

Liniendiagramm

Das Liniendiagramm ist Ihnen bereits aus der Schule bekannt. Hier wird die Verteilung einer Variablen durch Punkte dargestellt, die dann durch eine Linie verbunden werden. Mit Liniendiagrammen können u.a. Verteilungen dargestellt werden. Der Vorteil zum Histogramm ist hier, dass Sie auch bisher unbekannte Zwischenwerte ablesen können, sofern dies sinnvoll möglich ist.

Beispiel:

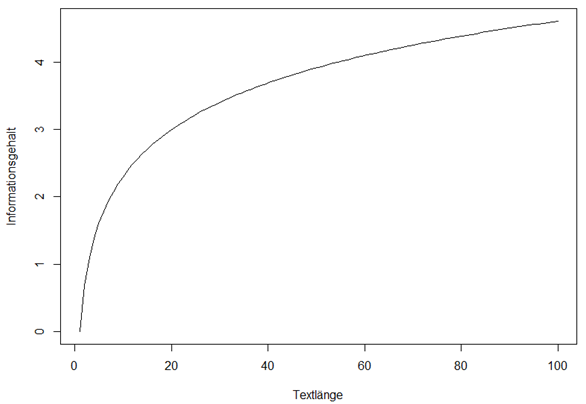
Ein fiktives Beispiel für ein Liniendiagramm ist unten dargestellt. Sie können sich vorstellen, dass hier die Seitenzahl eines Textes gezählt wurde und der Informationsgehalt des Textes auf einer Skala von 0 (= sehr gering) bis 5 (= sehr hoch) eingestuft wurde. Das Verhältnis von Textlänge und Informationsgehalt kann in der Grafik abgelesen werden. Bei einer Textlänge von 0 Seiten war der Informationsgehalt 0, bei einer Textlänge von 10 Seiten ungefähr 2.3, bei einer Textlänge von 20 ungefähr 3. Am Anfang steigt der Informationsgehalt steil an, der Unterschied des Informationsgehalts zwischen 80 und 100 Seiten ist nur noch sehr gering.

Box-Plot

Ein Box-Plot stellt die Verteilung einer Variablen auf andere Weise als Liniendiagramme oder Histogramme dar. Im Box-Plot werden nicht die Daten direkt oder in Häufigkeiten, sondern die schon berechneten Kennwerte (Median, Minimum, Maximum, unteres/ oberes Quantil) dargestellt.

Das Beispiel wurde wieder aus der Variable Alter des Datensatzes in diesem Beitrag gebildet:

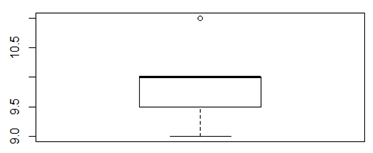
Der dicke Balken in der Mitte stellt den Median dar. Außerdem sind das obere und untere Quartil eingezeichnet. Das untere Quartil markiert die Grenze, ab der sich mehr als 25% der Werte befinden, das obere Quartil die Grenze, ab der sich mehr als 75% der Werte befinden. Diese Grenzen werden zu einer Box verbunden, sodass sich in der Box 50 % aller Werte befinden. Die sogenannten „Whiskers“ (hier nur unterer Balken) zeigen das Minimum und das Maximum an, wenn diese nicht mehr als 1.5 des Interquartilabstands vom Median entfernt sind. Als Interquartilabstand wird der Abstand zwischen dem unteren und dem oberen Quartil bezeichnet. Kleine Kreise sind Ausreißer, die mehr als 1.5 des Interquartilabstands vom Median entfernt sind. Im Beispiel hat also das Maximum einen größeren Abstand zum Median und ist deshalb als Ausreißer und nicht als Whisker eingezeichnet.

Problemquellen

Bei der Erstellung von Grafiken (und natürlich auch bei der Interpretation) ist es wichtig, einige Aspekte zu beachten, die zu Problemen führen könnten.

1. Beginnt die y-Achse bei 0? Wie das folgende Beispiel verdeutlicht, sollte immer der Startpunkt der y-Achse beachtet werden. In beiden Grafiken werden die gleichen Daten wiedergegeben, in der linken könnte ein großer Unterschied zwischen den Gruppen vermutet werden, wohin der (gleiche) Unterschied in der rechten Grafik vergleichsweise klein wirkt. Ehrlicher ist also die Verwendung des rechten Diagramms.
   
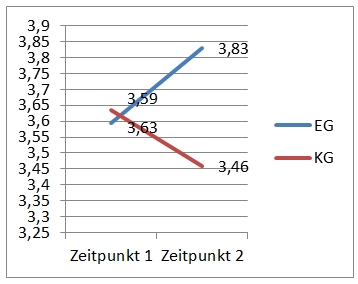
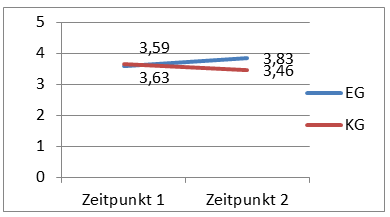
2. Wurden bestimmte Diagrammelemente weggelassen oder hervorgehoben, z.B. die Beschriftung der Achsen? Auch hier hilft das Beispiel von oben: Stellen Sie sich vor, im linken Diagramm wären die y-Achse und die Punkte nicht beschriftet. Es könnte nicht festgestellt werden, wie groß der Unterschied ist und dadurch würde er größer als tatsächlich wirken.
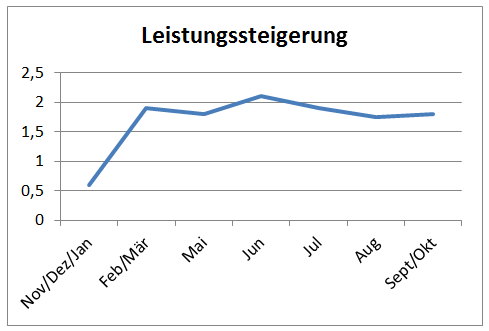
3. Sind die Abstände auf der Größenachse durchgängig gleich? Wenn ein Wechsel auf der Größenachse stattfindet (z.B. Wechsel von Sekunden zu Minuten), kann die Grafik nicht mehr auf einen Blick angemessen interpretiert werden, da sie verzerrte Werte darstellt. Das folgende Beispiel zeigt die Leistungssteigerung einer Schülerin innerhalb eines Jahres. Einige Monate sind zusammengefasst, während andere einzeln aufgeführt werden. Obwohl die Leistungssteigerung in diesem Fall zum Ende des Jahres abnimmt, sieht es so aus, als würde die Leistungssteigerung im September und Oktober gleich bleiben.

Software-Empfehlungen:

Tabellenkalkulationsprogramme wie bspw. Microsoft Excel oder Open-Office helfen Ihnen dabei, Grafiken zu erstellen. Auch weitere Statistik-Software wie SPSS oder auch die R bieten Funktionen zur Erstellung von Diagrammen.

https://www.youtube.com/watch?list=PLqzoL9-eJTNBDdKgJgJzaQcY6OXmsXAHU&v=cX532N_XLIs

Literatur:

Beller, S. (2008). Empirisch forschen lernen. Konzepte, Methoden, Fallbeispiele, Tipps (2., überarb. Aufl). Bern: Huber.

Bortz, J. & Schuster, C. (2010). Statistik für Human- und Sozialwissenschaftler (7. Aufl.). Berlin: Springer.

Krämer, W. (2009). So lügt man mit Statistik (12. Aufl.). München: Piper.