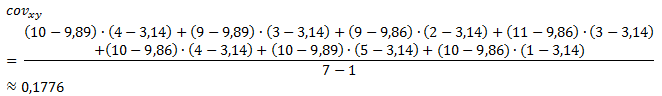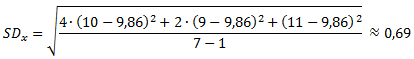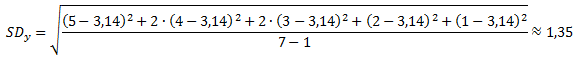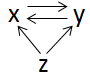Carla Bohndick

 

Wenn Sie untersuchen wollen, ob Zusammenhänge zwischen zwei Variablen bestehen, berechnen Sie die Korrelation. Zunächst ist dies eine deskriptive Fragestellung. Sie können die verschiedenen Zusammenhangsmaße aber auch inferenzstatistisch absichern. In diesem Kapitel wird verdeutlicht, was unter einer Korrelation verstanden wird. Außerdem werden Interpretationsprobleme dargestellt.

Die am häufigsten verwendete Möglichkeit, Zusammenhänge zwischen zwei Variablen zu berechnen, ist die Produkt-Moment-Korrelation. Um diese zu berechnen, müssen beide Variablen mindestens intervallskaliert sein. Im Folgenden berechnen wir die Korrelation zwischen dem Alter und der Motivation, genauer der Variable Mot 1 aus diesem Beitrag.

Zunächst müssen Sie die Kovarianz berechnen, die Formel dafür lautet:

Wenn Sie diese Formel genauer betrachten, fällt Ihnen sicherlich die Ähnlichkeit zu der in diesem Beitrag vorgestellten Varianz auf. Die Varianz ist nämlich lediglich die Kovarianz einer Variablen mit sich selber, also statt y würden Sie hier x einsetzen und so käme das Quadrat ins Spiel. Für unser Beispiel lässt sich also folgende Kovarianz berechnen:

Sei x = Alter und somit y= Mot1. Zuerst berechnen wir die Mittelwerte der Variablen x und y:

Nun können wir die Kovarianz berechnen:

Wir erhalten für unser Beispiel also eine Kovarianz von ca. 0,1776. Grundsätzlich kann die Kovarianz beliebig große Werte annehmen. Positive Werte sprechen dabei für einen positiven Zusammenhang zwischen den beiden Variablen und negative Werte für einen negativen Zusammenhang. Für unser Beispiel heißt das also, dass ein positiver Zusammenhang besteht.

Besser als die Kovarianz lässt sich die Korrelation (r) interpretieren. Für die Korrelation wird die Kovarianz anhand der Standardabweichungen (vgl. hier) der beiden Variablen standardisiert:

Zur Erinnerung: Die Standardabweichung ist gleich der Wurzel der Varianz.

Die Berechnung für unser Beispiel sieht also wie folgt aus:

Somit können wir r wie folgt berechnen:

 

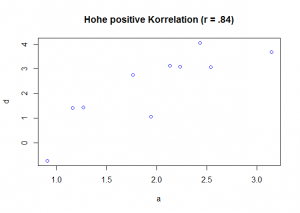
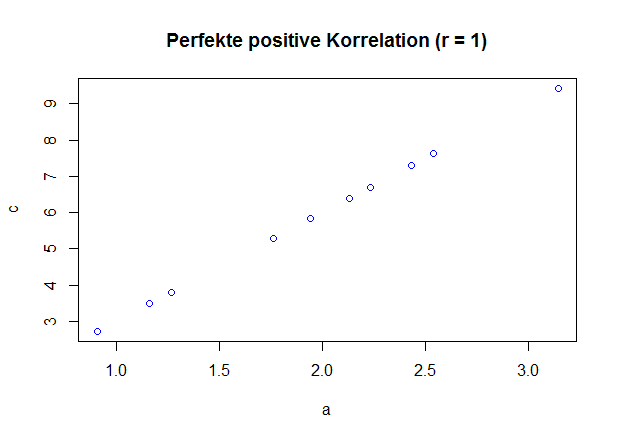
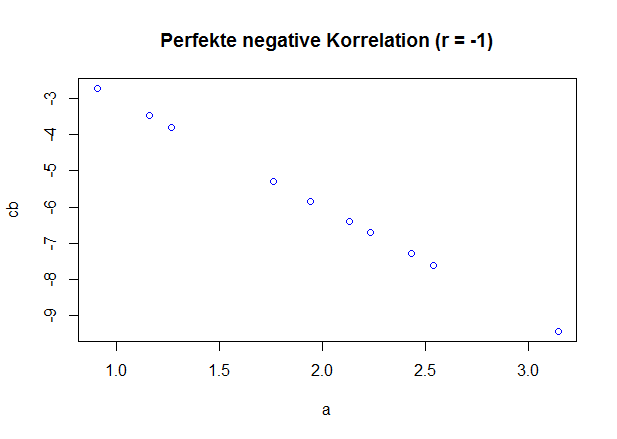
Der Korrelationskoeffizient r kann Werte von -1 bis 1 annehmen. Bei -1 liegt ein perfekt negativer Zusammenhang vor, bei 0 liegt kein (linearer) Zusammenhang vor und bei 1 liegt ein perfekt positiver Zusammenhang vor. Welche Korrelationen als groß und welche Korrelationen als klein bezeichnet werden, lässt sich nicht abschließend bestimmen. Einige Autoren sehen Korrelationen ab 0.5 als groß, Korrelationen um 0.3 als moderat und Korrelationen um 0.1 als klein (Cohen, 1988), andere hingegen sehen Korrelationen bis 0.5 als gering, 0.7 als moderat und 0.9 als hoch an (Nachtigall & Wirtz, 2004). Letztlich kommt es auf den publizierten Forschungsstand zu einer konkreten Fragestellung an, welche Werte als bedeutsam betrachtet werden. Im sozialwissenschaftlichen Bereich ist es für neue Forschungsfragen üblich, von der genannten Konvention nach Cohen auszugehen. Für unser Beispiel gehen Sie bitte davon aus, dass Werte ab 0.3 als bedeutsam angesehen werden können. Das heißt also, dass zwischen dem Alter und der Variable Mot1 ein geringer positiver Zusammenhang besteht.

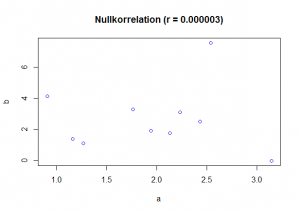
Um die verschieden starken Korrelationen besser zu illustrieren, finden Sie in den Abbildungen unten Beispiele für mögliche Korrelationen. Jeder Datenpunkt kann dabei einer Versuchsperson zugeordnet werden und zeigt damit das Ergebnis für zwei verschiedene Variablen an. Dabei ist die eine Variable auf der x-Achse und die andere Variable auf der y-Achse abgetragen.

   

   

 

Abb. 1 Verschiedene Korrelationen, Bewertung nach Cohen (1988)

Interpretationsprobleme: Korrelation und Kausalität

Stellen Sie sich vor, Sie hätten nun die Korrelation zwischen Leseleistung und Lesemotivation errechnet. Herausgekommen wäre r = 0.5, also ein moderater Zusammenhang zwischen den beiden Variablen. Sie können nun allerdings keine Aussagen über die Richtung des Zusammenhangs treffen. Das heißt, Aussagen wie „eine höhere Leseleistung führt zu einer höheren Lesemotivation“ oder andersherum „eine höhere Lesemotivation führt zu einer höheren Leseleistung“ sind nicht zulässig. Um Wirkrichtungen festzustellen, bedarf es spezieller Designs (vgl. Kapitel zur Planung). Manchmal ist auch eine dritte Variable z Auslöser für den Zusammenhang. Hier könnte z.B. die Begeisterung der Eltern für das Lesen (z) sowohl einen Einfluss auf die Lesemotivation (x) und auf die Leseleistung (y) haben, wie auch die folgende Abbildung veranschaulicht.

Um die Problematik zu verdeutlichen, sehen Sie im Folgenden weitere Beispiele, in denen fälschlicherweise eine bestimmte Richtung des Zusammenhangs angenommen wurde. Versuchen Sie doch einmal, die Gründe zu finden, die zu dem jeweiligen Zusammenhang geführt haben.

• Je mehr Leute der Feuerwehr eingesetzt werden, desto höher ist später der Brandschaden.
• Je größer die Füße, desto größer das Gehalt.
• Gute Luft (z.B. in Kurorten) führt zu einer erhöhten Sterblichkeitsrate.

 

Software-Empfehlungen:

Sie können Korrelationen per Hand berechnen, aber es gibt auch Computerprogramme, die Sie bei der Berechnung unterstützen können. Dies sind beispielsweise einfache Tabellenkalkulationsprogramme wie z.B. Excel, Sie können aber auch spezielle Software wie SPSS (kostenpflichtig) oder R (Open Source und kostenfrei) nutzen.

 

Literatur:

Beller, S. (2008). Empirisch forschen lernen. Konzepte, Methoden, Fallbeispiele, Tipps (2., überarb. Aufl). Bern: Huber.

Cohen, J. (1988). Statistical power analysis for the behavioral sciences (2. Aufl.). Hillsdale: L. Erlbaum Associates.

Krämer, W. (2009). So lügt man mit Statistik (12. Aufl.). München: Piper.

Nachtigall, C. & Wirtz, M. A. (2004). Wahrscheinlichkeitsrechnung und Inferenzstatistik (3. Aufl.). Weinheim: Juventa Verlag.