Carla Bohndick
Die deskriptive Statistik hilft Ihnen dabei, Ihre gesammelten Daten übersichtlich und anschaulich zusammenzufassen. Stellen Sie sich beispielsweise vor, Sie haben in Ihrer Befragung die demografischen Angaben Ihrer Versuchspersonen erhoben, vielleicht durch einen Fragebogen. Die deskriptive Statistik bietet Ihnen Kennwerte, die Ihnen dabei helfen, die Ergebnisse verdichtet darzustellen. Stellen wir uns also weiter vor, Sie haben das Alter Ihrer Versuchspersonen erhoben. Lagemaße (auch: Maße der zentralen Tendenz) geben nun an, welches Alter die Stichprobe am besten charakterisiert. Streuungsmaße (auch: Maße der Variabilität) zeigen die Unterschiedlichkeit der Stichprobe an.
Lagemaße
Die drei gebräuchlichsten Lagemaße sind das arithmetische Mittel, der Median und der Modus:
- Modus: definiert als derjenige Messwert, der am häufigsten in der Stichprobe vorkommt.
- Median: definiert als der Wert, der die Stichprobe in zwei Hälften teilt, wobei 50 % der Stichprobe größere (bzw. gleiche) Werte und 50% kleinere (bzw. gleiche)Werte aufweisen.
- Arithmetisches Mittel („Durchschnitt“): definiert als Summe der Werte in der Stichprobe, geteilt durch die Anzahl dieser Werte.
Streuungsmaße
- Range (Spannweite): Bereich vom kleinsten bis zum größten Wert, der in der Stichprobe auftritt
- Varianz: Mittelwert der quadrierten Abweichungen aller Einzelwerte vom Mittelwert der Verteilung (große Werte sprechen für eine hohe Unterschiedlichkeit der Messwerte in der Stichprobe, kleine für ähnliche Messwerte in der Stichprobe):
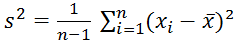
- Standardabweichung: Wurzel der Varianz (die Interpretation der Standardabweichung ist einfacher als die der Varianz, da die Werte in der gleichen Einheit wie die der Messwerte verstanden werden können):
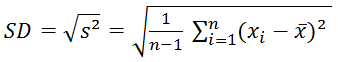
Die Wahl des Lagemaßes und des Streuungsmaßes hängt vom Skalenniveau des gemessenen Merkmals, also der Variable ab:
| Skalenniveaus | Erklärung | Beispiel | Lagemaß | Streuungsmaß |
| Nominal | Keine sinnvolle Reihenfolge | Geschlecht (männlich, weiblich) | Modus | – |
| Ordinal | Reihenfolge möglich Kein gleicher Abstand |
Schulform (Hauptschule, Realschule, Gymnasium) | Modus, Median | Range |
| Metrisch (Intervall- & Verhältnisskala) | Reihenfolge möglich Gleicher Abstand |
Alter (9 Jahre, 10 Jahre, …) | Modus, Median, Mittelwert | Range, Varianz, Standardabweichung |
Beispiel
Hier sehen Sie einen Ausschnitt aus einer Befragung zum Thema Motivation:
| Nr | Geschlecht | Alter | Schulform | Mot1 | Mot2 | Mot3 | Mot4 | |
| 1 | W | 10 | Gy | 4 | 4 | 5 | 5 | |
| 2 | M | 9 | Real | 3 | 4 | 3 | 4 | |
| 3 | M | 9 | Haupt | 2 | 1 | 2 | 2 | |
| 4 | M | 11 | Real | 3 | 2 | 3 | 3 | |
| 5 | W | 10 | Gy | 4 | 3 | 3 | 4 | |
| 6 | W | 10 | Real | 5 | 4 | 5 | 5 | |
| 7 | W | 10 | Gy | 1 | 2 | 2 | 1 |
Zunächst müssen Sie die Skalenniveaus bestimmen:
- Nominal: Geschlecht
- Ordinal: Schulform
- Metrisch: Alter, Klasse, Mot1-Mot4
Anschließend können Sie die Lagemaße errechnen (hier der jeweils höchstwertigste):
- Geschlecht: W: 4 x vertreten; M: 3 x vorhanden; Modus: weiblich, d.h. die Mehrheit der befragten Personen ist weiblich. Weiblich ist also der Modalwert (= Modus).
- Alter:
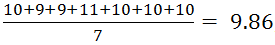 ;
;
arithmetisches Mittel, d.h. im Schnitt sind die befragten Personen 9,86 Jahre alt - Schulform: Zunächst wird jeder Schulform ein Wert zugeordnet, Hauptschule wird mit 1 und Gymnasium mit 3 belegt. Anschließend werden die Werte der Reihenfolge nach sortiert: 1,2,2,2,3,3,3. Der Wert in der Mitte ist der Median = 2, d.h. mindestens die Hälfte der Schüler/-innen ist mindestens auf der Realschule
- …
Schließlich berechnen Sie (wenn möglich) die Streuungsmaße:
- Geschlecht: –
- Alter:
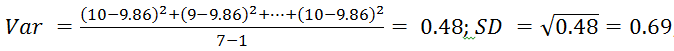 ,
,
d.h. die durchschnittliche Abweichung des Alters vom Mittelwert 9.86 beträgt 0.69 Jahre.
 ,
,
d.h. die jüngste Person ist 2 Jahre jünger als die älteste - Schulform:
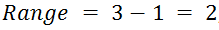 ,
,
d.h. die Person in der höchsten Schulform ist zwei Schulformen über der Person in der niedrigsten Schulform - …
Software-Empfehlungen:
Sie können deskriptive Statistiken zwar per Hand berechnen, sobald Sie aber eine größere Stichprobe haben, wird dies relativ aufwendig. Daher empfiehlt es sich zumindest Tabellenkalkulationsprogramme wie bspw. Microsoft Excel oder Open-Office zu nutzen. Hier können Sie die Formeln „programmieren“, häufig stehen Ihnen aber auch bereits passende Funktionen zur Verfügung.
Sollten Sie besonderen Spaß an Statistik haben oder gerne weitere Berechnungen durchführen wollen, gibt es dafür spezielle Programme. Weit verbreitet sind dabei das kostenpflichtige Programm SPSS oder auch die kostenlose Open Source Statistik-Software R.
Literatur:
Beller, S. (2008). Empirisch forschen lernen. Konzepte, Methoden, Fallbeispiele, Tipps (2., überarb. Aufl). Bern: Huber.
Bortz, J. & Schuster, C. (2010). Statistik für Human- und Sozialwissenschaftler (7. Aufl.). Berlin: Springer.
